搜索 登录注册
×

热门关键词：Web前端|前端开发|HTML5|CSS3|jQuery|CSS3动画

【SVG】纯clip-path打造的3D模型渲染器

作者：Terry2016.09.25来源：Web前端之家浏览：18336评论:0
关键词：html5SVG

               几天之前, 一个species-in-pieces的网站把我震到了(如下图), 出于一个优秀前端的敏锐嗅觉和原始本能， 我立刻祭出了看家法宝——Chrome开发者工具开始偷窥这个网站.

species-in-pieces

简单推敲之后，我发现其实原理可以归结为一个属性--clip-path, 又一篇博文的材料到手！ 当我兴高采烈的将我的《Species in Pieces原理解析》进行到一半时，发现First blood在weibo上已经被人抢了.

species-in-pieces

几乎在崩溃的同时，我突然意识这个属性其实可以用来更酷的事情, 即：

渲染3D模型

由浅入深的传统不能破，我们还是先简单来回顾下clip-path这个属性.

clip-path初见

既然要讲clip-path, 我们就不得不提clip, 它可以选择显示一个矩形区域.

#middle {
   left: 280px;
   clip: rect(119px, 255px, 229px, 80px);
   /* standard syntax, unsupported by Internet Explorer 4-7 */
}

#bottom-right {
   left: 200px;
   clip: rect(235px 335px 345px 160px);
   /* non-standard syntax, but supported by all major browsers*/
}

缺陷显而易见，它只能裁剪矩形区域。这个属性目前已经被 deprecated, 因为我们有了更强大的clip-path.

clip-path 用来显示一个特殊的路径, 所有裁剪路径内的内容才会被显示。

这个属性支持CSS Shape Module Level 1的图形定义, 例如(示例来自于css-trick)

.cliped{
  /* 圆 */
  clip-path: circle(30px at 35px 35px);

  /* 椭圆 */
  clip-path: ellipse(65px 30px at 125px 40px);
}

其实CSS和SVG在很多方面有着千丝万缕的关系, Masking Module规范(clip-path隶属)基本源自于SVG. 所以支持SVG的clipPath来定义裁剪图形也丝毫都不奇怪了, 如下例所示

.cliped{
  /* 本页的内联svg */
  clip-path: url(#c1);

  /* 远程svg信息, c1代表的是id */
  clip-path: url(path.svg#c1);
}

对应的<clipPath>节点.

<clipPath id="clipping">
  <circle cx="150" cy="150" r="50" />
  <rect x="150" y="150" width="100" height="100" />
</clipPath>

今天我们会提到的图形定义主要是多边形polygon, 这也是最为灵活的一种图形描述方式, 例如下图

species-in-pieces

利用以下代码(兼容非IE浏览器)裁剪后

.clip{
    /*Chrome,Safari*/
    -webkit-clip-path: polygon(647px 409px,840px 203px,619px 12px,418px 213px);

    /*Firefox*/
    clip-path: url("#clipPolygon");

    /* iOS support inline encoded svg file*/
    -webkit-mask: url(data:image/svg+xml;charset=utf-8;base64,PD94bWwgdmVyc2lvbj0iMS4wIiBlbmNvZGluZz0iVVRGLTgiIHN0YW5kYWxvbmU9Im5vIj8+CjwhRE9DVFlQRSBzdmcgUFVCTElDICItLy9XM0MvL0RURCBTVkcgMS4xLy9FTiIgImh0dHA6Ly93d3cudzMub3JnL0dyYXBoaWNzL1NWRy8xLjEvRFREL3N2ZzExLmR0ZCI+CjxzdmcgeG1sbnM9Imh0dHA6Ly93d3cudzMub3JnLzIwMDAvc3ZnIiB2ZXJzaW9uPSIxLjEiIHdpZHRoPSIwIiBoZWlnaHQ9IjAiPgogIDxjbGlwUGF0aCBpZD0ic3ZnQ2xpcCI+CiAgICA8cGF0aCBpZD0ic3ZnUGF0aCIgZD0iTTY0Nyw0MDkgTDg0MCwyMDMgNjE5LDEyIDQxOCwyMTMgeiIvPgogIDwvY2xpcFBhdGg+CiAgPHBhdGggaWQ9InN2Z01hc2siIGQ9Ik02NDcsNDA5IEw4NDAsMjAzIDYxOSwxMiA0MTgsMjEzIHoiICAvPgo8L3N2Zz4=) no-repeat;
}

结果

species-in-pieces

对于firefox，我们需要用<clipPath>来定义图形.

<svg width="0" height="0">
  <clipPath id="clipPolygon">
    <polygon points="647 409,840 203,619 12,418 213">
    </polygon>
  </clipPath>
</svg>

clip-path完成的就是这样一个简单的工作， 但是恰恰解决了前端开发中一系列头疼的限制.

我们先从文章开始的《species in pieces》来剖析下clip-path的妙用吧.

借《species in pieces》深入学习clip-path

我们先来看下在《species in pieces》中每个动物的组成节点.

<div class="wrap left-to-right">
    <div class="shard-wrap">
        <div class="shard"></div>
    </div>
    <div class="shard-wrap">
        <div class="shard"></div>
    </div>
    .
    .
    省略若干30个
    .
    .
    <div class="shard-wrap">
        <div class="shard"></div>
    </div>
    <div class="shard-wrap">
        <div class="shard"></div>
    </div>
</div>

对应的部分关键css

.shard-wrap { 
    width: 100%; 
    height: 100%; 
    position: absolute; 
    transition: .5s; 
    z-index: 2; 
}

/* crow 乌鸦的图形描述 */
.crow .shard-wrap:nth-child(1) .shard {
    -webkit-clip-path: polygon(20% 50%,25% 52.4%,11.5% 54.5%);
    background-color: #2C323D
}
.crow .shard-wrap:nth-child(2) .shard {
    -webkit-clip-path: polygon(14.7% 47.5%,35.2% 50.2%,25% 52.5%);
    background-color: #63676F
}
.crow .shard-wrap:nth-child(3) .shard {
    -webkit-clip-path: polygon(22.9% 44.5%,35.2% 50.2%,25% 48.9%);
    background-color: #0F1622
}
/*
.
.
省略中间25个
.
.
*/
.crow .shard-wrap:nth-child(29) .shard {
    -webkit-clip-path: polygon(61.7% 44.7%,64.4% 44%,65.1% 36.2%);
    background-color: #0f1622
}
.crow .shard-wrap:nth-child(30) .shard {
    -webkit-clip-path: polygon(78.5% 21.5%,76.3% 23.7%,74.6% 22.5%);
    background-color: #0f1622
}

我们可以发现，每个动物其实都是由30个三角形组成的, 每个三角形就代表一对.shard-wrap>.shard节点, 它们都是100%的宽高的盒子.所以图形完完全全是通过clip-path:polygon裁剪而来的.

以上例的crow乌鸦为例，所有的图形描述其实都定义在CSS中, 由:nth-child伪类选择器来控制每一块三角的形状. polygon传入了三个参数即代表三角形的 三个顶点. 这里注意到由于是百分比单位， 图形天然就是响应式的, 创建的图形就像是SVG图形.

species-in-pieces

另外几个关键知识点

clip-path的碰撞盒

上面的这种绘图在体验上非常接近我们使用canvas, 但是虽然被裁减后，仿佛我们创造了其他的图形， 其实节点的碰撞盒(Bounding Box)仍然是原长方形, 这它仍然会和未裁剪时一样进行排版. 使得如果我们应用此项技术到游戏相关开发中时， 我们仍需要去实现一套对应的碰撞盒机制.

clip-path区域的UI响应

有些人可能会问， 这是否意味着，其实只是相当于: 将裁剪区域外的内容隐藏了， 而不是真正的剔除? 答案不完全正确, 因为clip-path实现了只有保留区域可以进行UI响应, 这使得裁剪图形更像是一个独立的个体。

clip-path可以触发Animation!

最关键的一点还没有提到的就是: 这些动物图形都是活动的, 但是这些动画并不是通过定时器去实现， 而是通过css动画!, 继续 深挖一下crow的其余css代码.

.shard{
    transition: -webkit-clip-path 0.6s;
}
/* state-two 状态二 */
.animal-animations-on.state-two .crow .wrap .shard-wrap:nth-child(1) .shard {
    -webkit-clip-path: polygon(44.7% 33.5%,65% 26.7%,65% 36.1%)
}
/**
.
.省略若干
.
*/
.animal-animations-on.state-two .crow .wrap .shard-wrap:nth-child(30) .shard {
    -webkit-clip-path: polygon(82.5% 26.5%,80.3% 28.7%,78.6% 27.5%)
}
/* state-three 状态三 */
.animal-animations-on.state-two .crow .wrap .shard-wrap:nth-child(1) .shard {
    -webkit-clip-path: polygon(86.57% 33.5%,63.44% 56%,65% 36.4%)
}
/**
.
.省略若干
.
*/
.animal-animations-on.state-two .crow .wrap .shard-wrap:nth-child(30) .shard {
      -webkit-clip-path: polygon(44.7% 34.5%,65% 28.7%,65% 36.1%)
}

我们会发现每种动物的各阶段造型都由父节点.animal-animations-on的全局类名state-x来控制, 这种方式能凑效的根本原因是: 动画在一定条件下可以对clip-path生效 . 这里的一定条件即: 裁剪的多边形必须具有相同的顶点数, 这其实也符合常理, 浏览器怎么知道你如何从三角形变换到四边形呢？

这里我们的第二个图形里， 将三角形也使用四个顶点来生成， 这样可以使得变换为四边形的时候可以进行动画。

《pecies in pieces》中那些些栩栩如生的动物拼图并没有蕴含什么复杂的技术问题， 微博的@周文彬1986同学将部分形状数据提取了出来 ，只利用了几行Sass代码就实现了简化效果. 所以这无论如何都称不上是一个技术性突破, 而是一个100%的充满灵感的图形和动效设计的典范， 有时还是不禁会唏嘘为什么我们想不到这种创意.

不过虽然在设计灵感上与别人相去甚远， 我们还可以在技术层面来进行不同的尝试. 比如, 完全利用clip-path实现一个3D模型的渲染器.

使用clip-path属性实现3D模型渲染器

这节我不会对所谓的计算机图形学做深入的探讨, 这是因为:

懂它的肯定比我懂，不懂的我也没法在一篇博文里解释清楚.

所以接下来的原理简要不会涉及到任意公式推导, 有兴趣的可以参考下clip3d的源码部分.

我们先来看个简单的例子:

通过DEMO， 我们会发现实际上它不涉及CSS用于变换的transform内容, 那它是怎么实现的呢？

3维坐标系

既然是3d图形， 当然在3维空间内会有一个唯一的定义， 就比如下图的Ag点， 它由x坐标、y坐标与z坐标组成.

事实上，在进行矩阵计算时,是四维齐次坐标

species-in-pieces

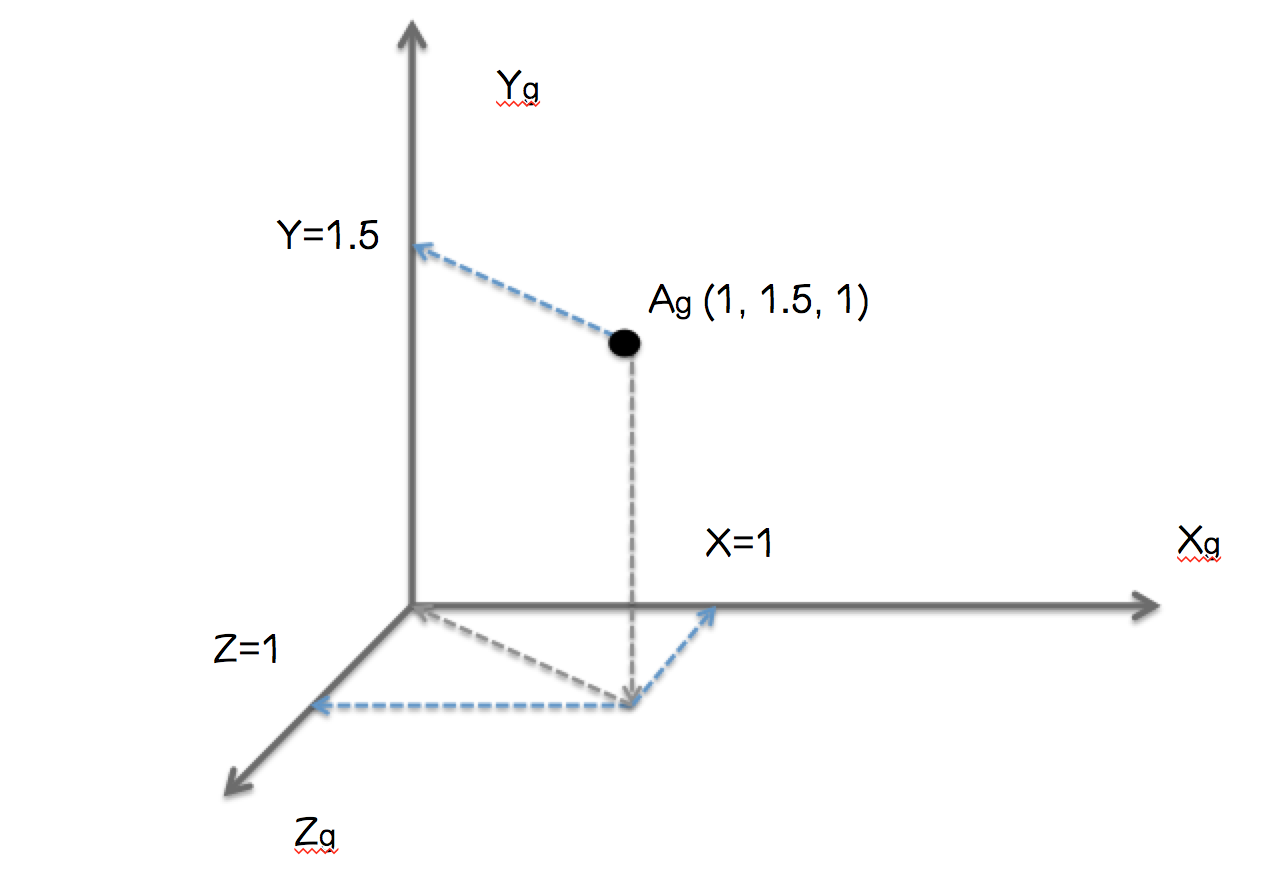
但是问题来了， 我们的窗口只能显示2维平面图形, 如何实现3D展示?

答案就是利用视觉透视原理的投影变换.

投影

天生的，我们对物体的直观感受是近大远小, 当我们将这种特性应用到二维绘图时， 它就具有真实自然的三维立体形态.

species-in-pieces

小插曲: 在google搜索“透视”的图片时，我惊呆了

透视投影与连续放映的图片由于视觉暂留效果看起来像是活动的一样， 都一种“视觉欺骗”.

从3D图形映射到我们的二维平面就称之为“投影”.

species-in-pieces

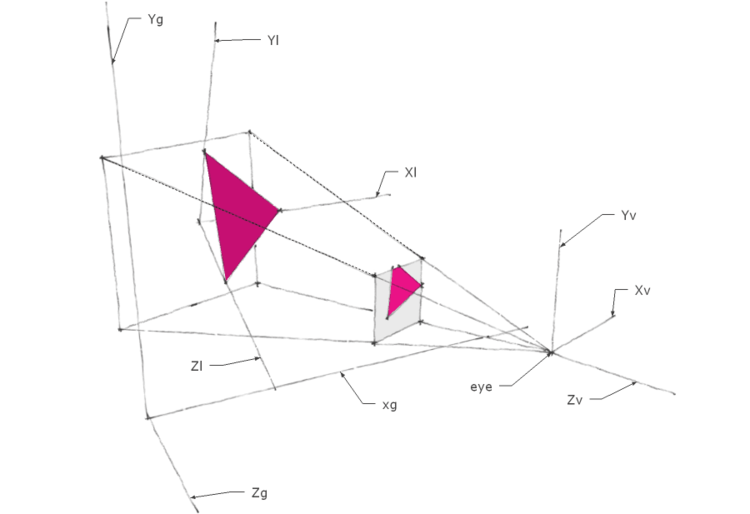
空间变换

以上图为例, 在三维空间的三角形到最终投影到屏幕中, 会先经过两次坐标系变换.

  • 物体空间到全局空间的空间转换, 如图中的L空间 -> G空间

  • 全局空间到摄像机空间(eye为原点的齐次空间)的空间转换, 如G空间 -> V空间

比如局部空间的顶点(1, 0, 0)到了全局空间可能就是(0, 1, 0), 这种变换都是通过矩阵运算来实现的.

当然你完全可以省去这两个步骤, 直接将模型定义在摄像机空间, 但是这样不利于模型的通用性, 事实上在复杂场景下， 从局部空间到全局空间往往需要多次变换.

投影变换

接下来就是摄像机空间到裁剪空间的投影变换了. 熟悉OpenGL的同学可能了解这个正是glPerspective和glFrustum所做的工作.

刚才图3中， 其实还定义了一个四棱台， 这个称之为“视椎体”, 它定义摄像机的最大可视距离, 最小可视距离(一般为投影面)以及可视角度, 只有在这个视锥体之内的物品是可以被显示的, 否则将会被剔除(或裁减).

投影变换实际上也是一次空间变换， 它将视锥体内的点映射到了标准化的立方体内(如图4), 坐标范围从[-1, -1, -1] 到 [1, 1, 1], 所有经过映射点如果落在立方体之外即代表它在视锥体之外.

species-in-pieces

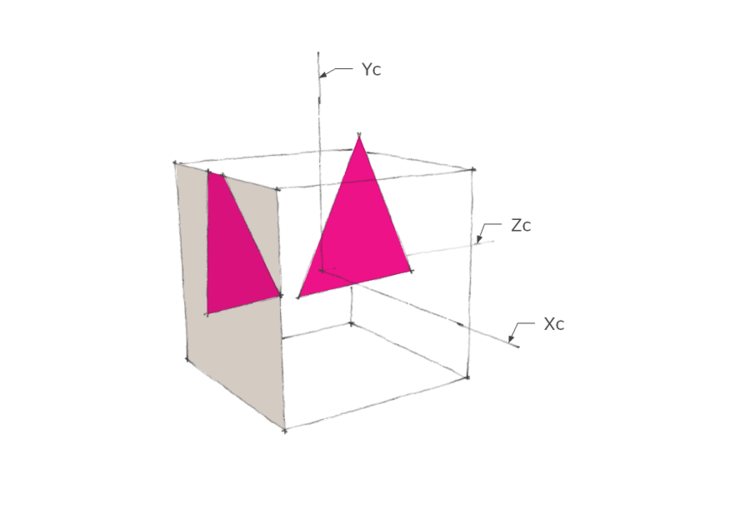
这么做带来的最终结果是： 近大远小的视锥体，变成了等宽等长的立方体。 这样所有标准体内的节点到投影面都是等值投影(不需要做近大远小处理)。

理论上我们只要将各个面包含的顶点的[x,y]坐标连接起来并填充成面，就可以完成物体的渲染了！ 实际上推广到Web前端实现， 我们还需要多做一步， 那就是:

荧幕坐标系到窗口坐标系的转换

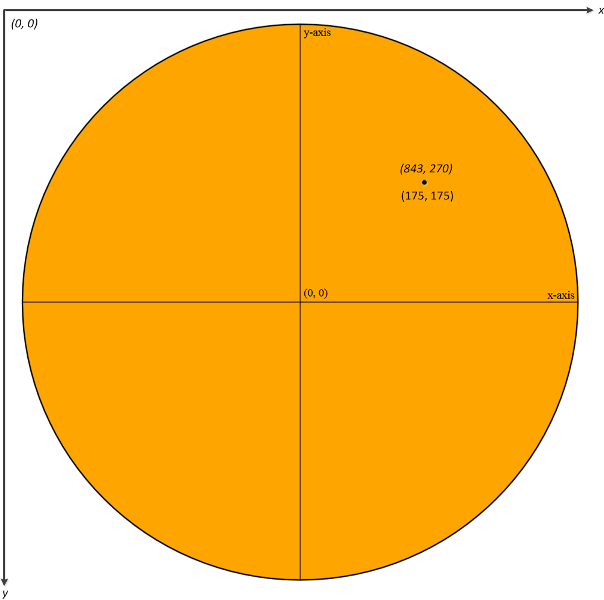
经过投影矩阵变换后， x/y轴的范围是[-1, 1]. z轴为[-1, 1]. 假设我们最终获得的某个三角形顶点位置为分别是[-0.2, 0.3, 0.5] ，[0.2, -0.3, 0.1] 和 [0.5, 0.5, 0.3]. 但由于中心点和坐标轴方向与Web浏览器的定义都完全不同， 如下图所示.

species-in-pieces

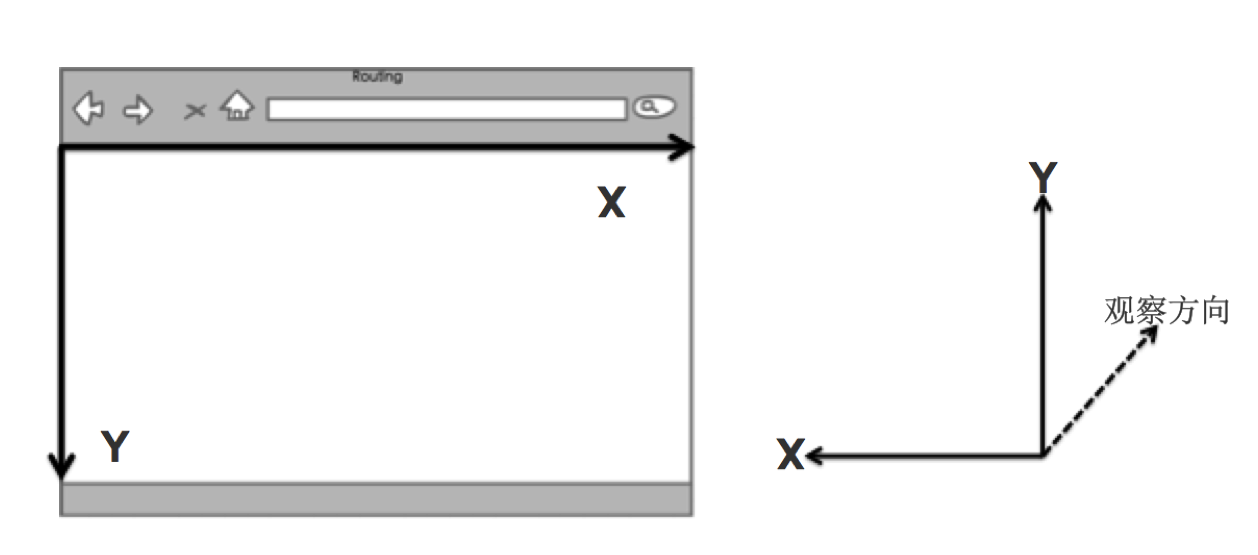
我们需要将x,y坐标修正到与窗口坐标系匹配.

x` = 0.5 - x
y` = 0.5 - y

即三个顶点分别为[0.7, 0.2, 0.5]、[0.3, 0.8, 0.1]和[0, 0, 0.3], 为避免计算, 我们换算到百分比坐标并取其x,y坐标利用clip-path渲染出对应的平面图形.

.face1{
  -webkit-clip-path: (70% 20%, 30% 80%, 0% 0%);
}

由于平面图形符合透视常识， 所以在视觉上你会感觉到这是个3D图形.

锦上添花.

z-sorting

其实我们发现，经过投影变换后， 得到的坐标是有z分量的, 它正是用来帮助我们处理3D下两个面“谁前谁后的问题”. 由于实现方案的天然限制, 我们是无法实现像素级的Z深度缓存的, 但是我们可以利用z-index来实现一个山寨的z-sorting, 我们首先记录一个面的平均深度(三顶点), 然后直接将其取负作为节点的z-index值就完成了深度排序了

背面剔除与光照

背面剔除与光照分别利用平面法线与观察方向和光线投射方向有关， 一些简单的三角函数+向量点积计算和色值混合操作， 这里我们就不再多做说明. 简单起见， 光源这里只处理为平行无限远的光源， 而背面剔除我们仅仅只是display:none而已

clip小节

使用clip-path尝试渲染3D 模型其实在绘图部分与之前的《pecies in pieces》并没有本质的不同:

它们都是由三角形组成的图形, 并且每个三角形是由div和clip-path实现的. 但是由于引入了透视投影, 使得clip-path有了渲染3D模型的能力。

别逗我了，CSS3不是早有transform 3d吗！

是的， 上面那个例子其实可以使用transform更简单的解决， 以正方体为例.

.back {
  transform: translateZ(-100px) rotateY(180deg);
}
.right {
  transform: rotateY(-270deg) translateX(100px);
  transform-origin: top right;
}
.left {
  transform: rotateY(270deg) translateX(-100px);
  transform-origin: center left;
}
.top {
  transform: rotateX(-90deg) translateY(-100px);
  transform-origin: top center;
}
.bottom {
  transform: rotateX(90deg) translateY(100px);
  transform-origin: bottom center;
}
.front {
  transform: translateZ(100px);
}

五面体的例子稍微复杂一点, 但仍然可以做， 即使用border来模拟出我们的三角形.

但是如果是下面这种例子呢？transform就束手无策了,

最关键的问题就是, 由于上文所提到的例子在流程上与常规意义上的3d渲染一致的，我们可以使用类似的数据模型来渲染图形。 而transform是以面为基础的， 有着天然的劣势。

例如DEMO1的数据其实来自于著名的learningWebGL

var Render = clip3d.Render,
  Light = clip3d.Light,
  Camera = clip3d.Camera,
  vec3 = clip3d.vec3,
  mat4 = clip3d.mat4,
  _ = clip3d.util,
  color = clip3d.color;

var render = new Render({
  parent: document.getElementById("app"),
  camera: new Camera({
    eye: [4,4, -10]
  }),
  // simple point-lighting
  light: new Light({
    position: [ 0, 0, -1 ],
    color: [255, 255, 255,1]
  }),
  // http://learningwebgl.com/blog/?p=370
  // entity form learning webgl
  entities: [
    {
      vertices: [
        0,  1,  0,
        -1, -1, 1,
        1, -1,  1,

        0,  1,  0,
        1, -1,  1,
        1, -1, -1,

        0,  1,  0,
        1, -1, -1,
        -1, -1, -1,

        0,  1,  0,
        -1, -1, -1,
        -1, -1,  1,

        // warning the squence
        1, -1,  1,
        -1, -1, 1,
        -1, -1, -1,

        1, -1, -1,
        1, -1,  1,
        -1, -1, -1,

      ],
      colors: [
      ]
    },
    {
      vertices: [
  // Front face
      -1.0, -1.0,  1.0,
       1.0, -1.0,  1.0,
       1.0,  1.0,  1.0,
      -1.0,  1.0,  1.0,

      // Back face
      -1.0, -1.0, -1.0,
      -1.0,  1.0, -1.0,
       1.0,  1.0, -1.0,
       1.0, -1.0, -1.0,

      // Top face
      -1.0,  1.0, -1.0,
      -1.0,  1.0,  1.0,
       1.0,  1.0,  1.0,
       1.0,  1.0, -1.0,

      // Bottom face
      -1.0, -1.0, -1.0,
       1.0, -1.0, -1.0,
       1.0, -1.0,  1.0,
      -1.0, -1.0,  1.0,

      // Right face
       1.0, -1.0, -1.0,
       1.0,  1.0, -1.0,
       1.0,  1.0,  1.0,
       1.0, -1.0,  1.0,

      // Left face
      -1.0, -1.0, -1.0,
      -1.0, -1.0,  1.0,
      -1.0,  1.0,  1.0,
      -1.0,  1.0, -1.0
      ],
      indices : [
        0, 1, 2,      0, 2, 3,    // Front face
        4, 5, 6,      4, 6, 7,    // Back face
        8, 9, 10,     8, 10, 11,  // Top face
        12, 13, 14,   12, 14, 15, // Bottom face
        16, 17, 18,   16, 18, 19, // Right face
        20, 21, 22,   20, 22, 23  // Left face
      ],
      itemSize: 3,
      // for simplify. one face only have one color
      colors: [
        [255, 0, 0, 1],
        [255, 0, 0, 1],
        [255, 255, 0, 1],
        [255, 255, 0, 1],
        [0, 255, 0, 1],
        [0, 255, 0, 1],
        [255, 120 , 255, 1],
        [255, 120 , 255, 1],
        [120, 255, 0, 1],
        [120, 255, 0, 1],
        [0, 255, 120, 1],
        [0, 255, 120, 1]
      ],
      matrix: mat4.createRotate([0,0,1], 30)
    }
  ]
})

即一套模型数据可以应用于不同的环境， 只要我们使用标准化的Render即可， 这是transform所替代不了的。

clip3d的限制

  • 无法引入材质： 这点几乎判了这个clip-path的死刑了, 并且z-sorting是基于面的z-index, 是是有可能出现bug的

  • 性能: 超过1000个面在动画时就有了明显的卡顿

  • 浏览器支持度不佳: 比canvas更差

后记

聪明的朋友可能发现了， 本文其实只是一次3D pipeline操作的简单实现, 关键点其实就是”任意多边形”的渲染能力, 而clip-path恰恰是将我们从只能渲染长方形的尴尬境地中解放了出来，使得Web设计实现上有了更大的可能性.

同理可证前端还有这些平台可以实现这种级别的渲染器.

  • canvas/2d

  • canvas/webgl

  • svg

  • 快死的vml,flash

所有的代码都放在github: clip3d中，有兴趣的可以关注一下。

赏您的支持是我们创作的动力！
温馨提示：本文作者系Terry ，经Web前端之家编辑修改或补充，转载请注明出处和本文链接：
https://jiangweishan.com/article/svg1474732800887.html

网友评论文明上网理性发言 已有0人参与

发表评论:

相关文章